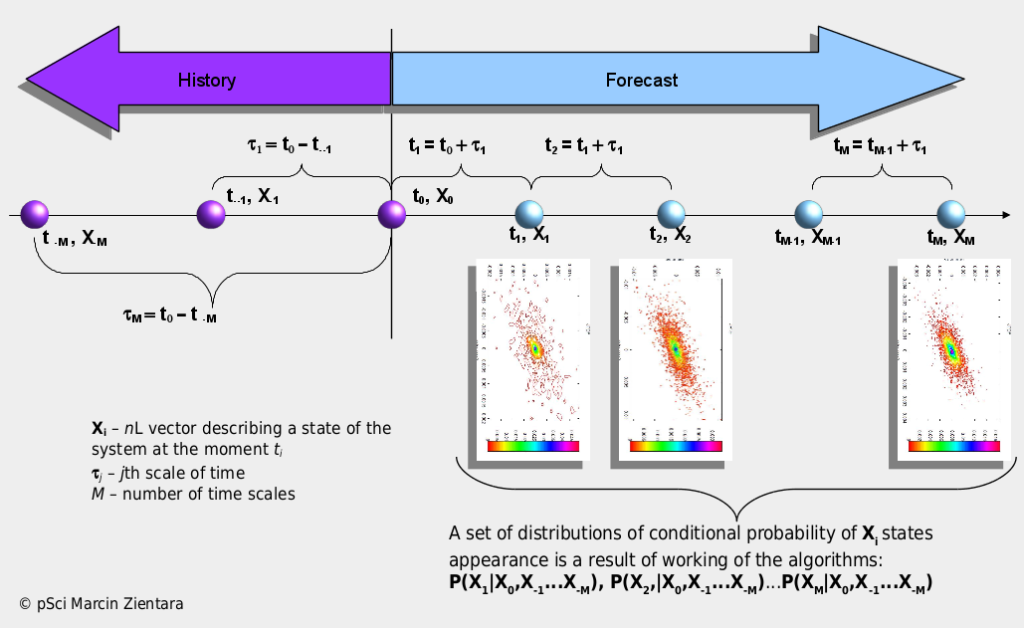
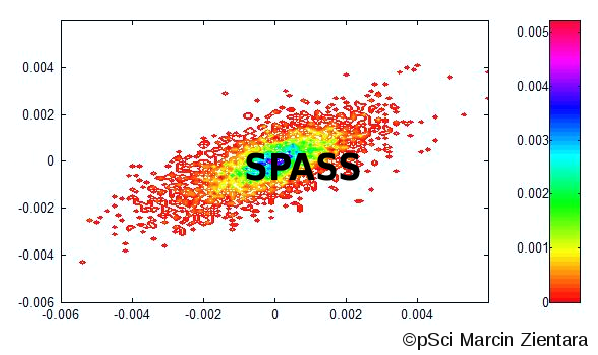
System Analizy i Symulacji Procesów Stochastycznych (SPASS) – jest to zbiór oryginalnych bibliotek programistycznych do zaawansowanej analizy, symulacji i prognozowania procesów stochastycznych opisanych szeregami czasowymi lub polami prawdopodobieństwa. Bazuje on na modelach pochodzących z fizyki statystycznej uzupełnionymi o teorie układów dynamicznych i informacji oraz metody AI i Big Data. Jest on wynikiem własnych prac badawczych w obszarze własności fizycznych układów złożonych oraz dostępnej, współczesnej literatury naukowej na ten temat. System umożliwia obiektywną wielowymiarową i wielkoskalową analizę i symulację ewolucji układów opisanych wielkościami stochastycznymi. Przez wielowymiarowość należy rozumieć postać zdarzenia losowego X, któremu przypisywana jest wartość prawdopodobieństwa wystąpienia. Zdarzenie to ma postać wektora o długości N (jest to liczba wymiarów), którego elementami mogą być np. różne pary walutowe, zbiór cech opisujących rynek energii X = (cena kontraktu, podaż/popyt energii) lub zbiór cech opisujących pracę maszyny X = (czujnik1, czujnik2, czujnik3). Przez wieloskalowość natomiast należy rozumieć badanie zmienności zdarzeń losowych X w kaskadzie kolejnych, coraz krótszych przedziałów czasu lub przestrzeni. Wszystkie niezbędne parametry konieczne do obliczeń wyliczane są ze ścisłych reguł matematycznych co stanowi przewagę SPASS nad innymi powszechnie używanymi systemami tego typu. Funkcjonalność SPASS znakomicie wpisuje się w koncepcje Przemysłu 4.0, Energetyki 2.0 oraz nowoczesnych rynków kapitałowych.
Zalety systemu SPASS:
- wszystkie parametry konieczne do symulacji i prognozowania wyliczane są ze ścisłych reguł ilościowych;
- system jest uniwersalny, brak założeń co do szczegółowej natury analizowanych procesów (fizyczne, społeczne, ekonomiczne itd.);
- prawdopodobieństwa łączne stanów/zdarzeń P(X1, X2, …Xn) (gdzie: X = (X1, X2, …Xn) jest wielowymiarową zmienną losową) wyliczane jest bezpośrednio a nie jako iloczyn P(X1)P(X2) …P(Xn). Dla systemów rzeczywistych najczęściej prawdziwa jest nierówność P(X1, X2, …Xn) ≠ P(X1)P(X2) …P(Xn). W wyniku stosowaniu iloczynu prawdopodobieństw jako oszacowania prawdopodobieństwa łącznego prowadzi do zbyt optymistycznych lub pesymistycznych wyliczeń;