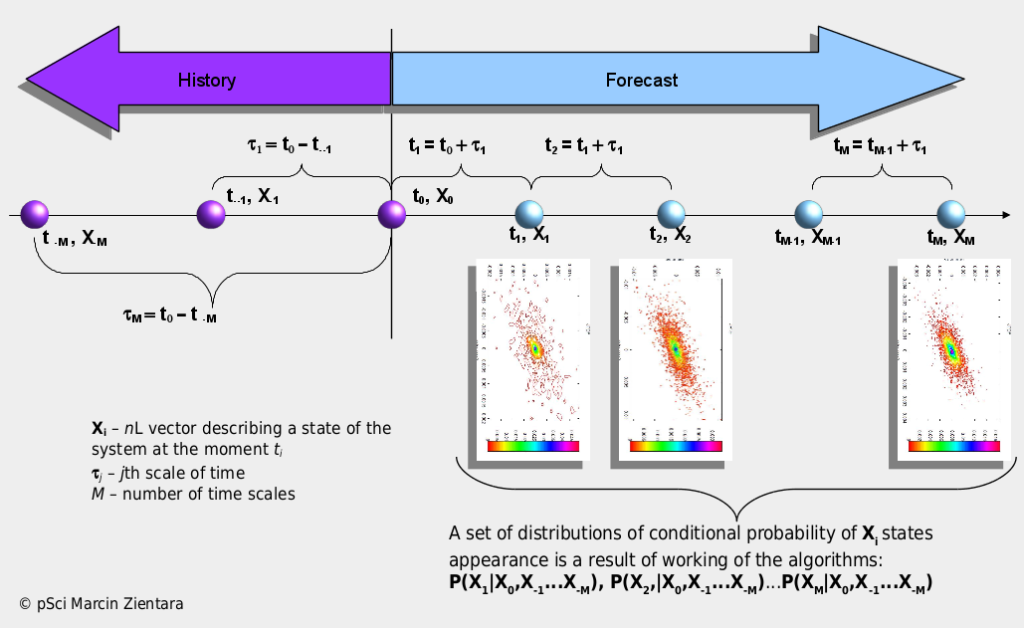
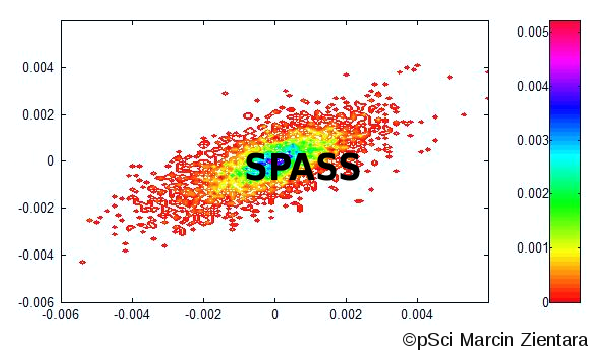
Stochastic Processes Analysis and Simulation System (SPASS) – is a collection of original programming libraries for advanced analysis, simulation and forecasting of stochastic processes described by time series or fields of probability. It is based on models from statistical physics supplemented with theories of dynamic systems and information as well as AI and Big Data methods. It is the result of own pSci research in the area of physical properties of complex systems and available, contemporary scientific literature on this subject. The system enables objective multidimensional and multiscale analysis and simulation of the evolution of systems described with stochastic values. By multidimensionality one should understand the form of a random event X, which is assigned the probability value of occurrence. This event is in the form of a vector with the length N (it is the number of dimensions), whose elements may be, for example, various currency pairs, a set of features describing the energy market X = (price of the contract, supply / demand of energy) or a set of features describing work of machine X = ( sensor1, sensor2, sensor3). Multiscale, on the other hand, should be understood as the investigation of the variability of random events X in the cascade of subsequent, ever shorter intervals of time or space. All necessary parameters for calculations are calculated from strict mathematical rules, which is an advantage of SPASS over other commonly used systems of this type. The SPASS functionality fits in perfectly with the concepts of Industry 4.0, Distributed Generation (Renewable Energetics ) and modern capital markets.
The main advantages of the SPASS system:
-
all parameters necessary for simulation and forecasting are calculated from strict quantitative rules;
-
the system is universal, there are no assumptions about the detailed nature of the processes being analyzed (physical, social, economic, etc.);
-
joint probabilities of states / events P (X1, X2,…Xn) (where: X = (X1, X2,…Xn) is a multidimensional random variable) is calculated directly, not as product P(X1)P(X2) …P(Xn). For real systems, the inequality of P(X1, X2, …Xn) ≠ P(X1)P(X2) …P(Xn) is most often true. In result, an application of the probabilities product as an estimate of the combined probability leads to too optimistic or pessimistic calculations ;